Representing Joint Hierarchies with Box Embeddings
Dhruvesh Patel, Shib Sankar Dasgupta, Michael Boratko, Xiang Li, Luke Vilnis, Andrew McCallum
Keywords: embeddings, order embeddings, knowledge graph embedding, relational learning, hyperbolic entailment cones, knowledge graphs, transitive relations
TLDR: Extending Box embeddings to model multiple relations
Abstract:
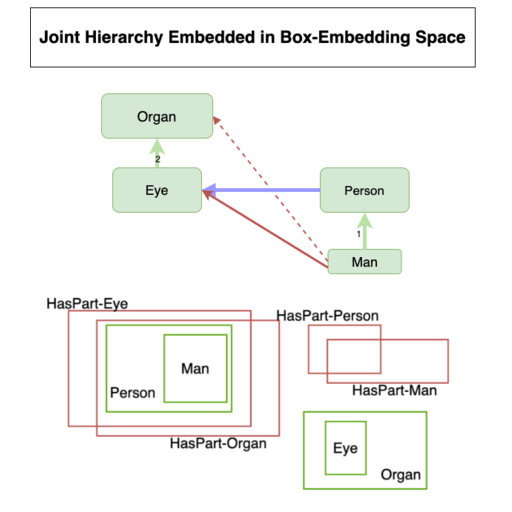
Learning representations for hierarchical and multi-relational knowledge has emerged as an active area of research. Box Embeddings [Vilnis et al., 2018, Li et al., 2019] represent concepts with hyperrectangles in $n$-dimensional space and are shown to be capable of modeling tree-like structures efficiently by training on a large subset of the transitive closure of the WordNet hypernym graph. In this work, we evaluate the capability of box embeddings to learn the transitive closure of a tree-like hierarchical relation graph with far fewer edges from the transitive closure. Box embeddings are not restricted to tree-like structures, however, and we demonstrate this by modeling the WordNet meronym graph, where nodes may have multiple parents. We further propose a method for modeling multiple relations jointly in a single embedding space using box embeddings. In all cases, our proposed method outperforms or is at par with all other embedding methods.